GORM 自动填充 UUID 的 2 种方式
目录
使用 uuid 库手动生成
采用这个库:github.com/gofrs/uuid
在 GORM 中定义一个 BaseModel,并增加钩子函数:
import "github.com/gofrs/uuid"
type BaseModel struct {
ID uuid.UUID
CreatedAt time.Time
UpdatedAt time.Time
DeletedAt gorm.DeletedAt `gorm:"index"`
EffectiveTime *time.Time
}
func (m *BaseModel) BeforeCreate() (err error) {
m.ID, err = uuid.NewV4()
if err != nil {
log.Logger.Err(err).Msg("uuid create failed")
return fmt.Errorf("uuid create with ID failed, %w", err)
}
return nil
}使用 postgresql 的 uuid-ossp 插件
首先要启用插件
要么手动 Navicat 界面上增加:
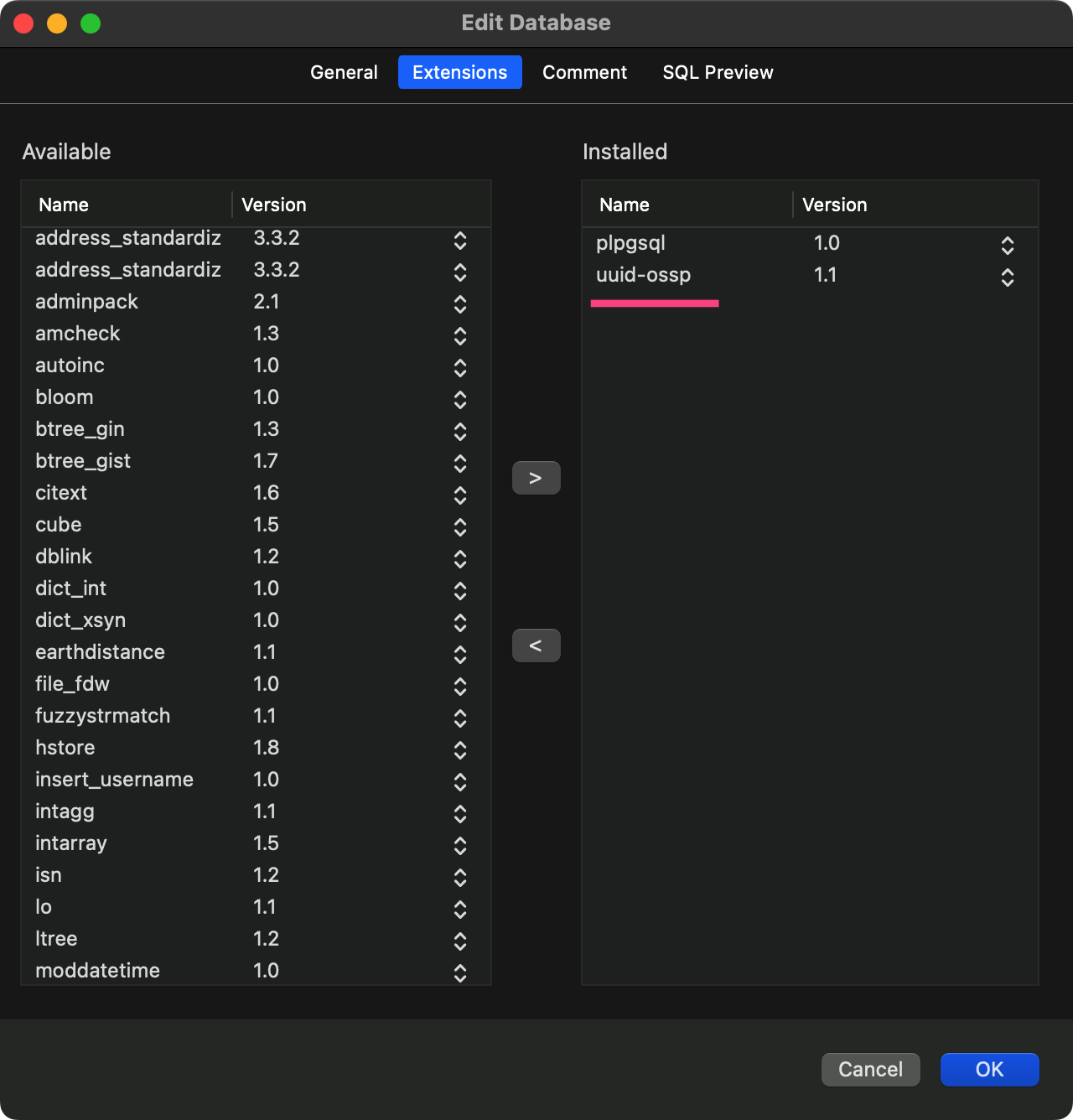
要么执行查询语句:
CREATE EXTENSION IF NOT EXISTS "uuid-ossp";
然后添加标签即可:
import "github.com/gofrs/uuid"
type Model struct {
ID uuid.UUID `gorm:"type:uuid;primary_key;default:uuid_generate_v4()"`
CreatedAt time.Time
UpdatedAt time.Time
DeletedAt gorm.DeletedAt `gorm:"index"`
EffectiveTime *time.Time
}使用另一个插件:pgcrypto
如果你只需要随机生成(版本4)的UUID,那么请考虑使用来自 pgcrypto 模块的
gen_random_uuid()函数。
这是官方文档说的,原因是 OSSP UUID库 已经没有很好维护了。
于是启用 pgcrypto 插件:
CREATE EXTENSION IF NOT EXISTS "pgcrypto";
然后添加标签:
import "github.com/gofrs/uuid"
type Model struct {
ID uuid.UUID `gorm:"type:uuid;primary_key;default:gen_random_uuid()"`
CreatedAt time.Time
UpdatedAt time.Time
DeletedAt gorm.DeletedAt `gorm:"index"`
EffectiveTime *time.Time
}更多 GORM 支持的字段标签
更多支持的标签字段请查看:https://gorm.io/zh_CN/docs/models.html#字段标签
参考文章
Example: golang gorm postgres uuid relation