动态连通性问题中的并查集
目录
著作权归作者 Handy 所有。商业转载请联系作者获得授权,非商业转载请注明出处。
简介
union-find 是为了解决动态连通性问题而提出来的一个算法,而对应的数据结构被称为并查集,集即集合。
动态连通性问题,可以联想到编程中两个变量名是否等价、集合中两个元素是否属于同一个集合、图中两个节点是否连通等。 简单地说,给你一些相连的节点对,让你判断一个新的节点对是否相连。
本文主要介绍核心的 union-find 算法,从最简单的 quick-find 到改进的 quick-union,再到 使用路径压缩的 quick-union,最后给出 使用路径压缩的加权 quick-union。
union-find 算法主要有三个函数:union(p,q)、find(p)、connected(p,q)。
- union:合并,将两个节点相连
- find:查找,找出节点所在连通分量(或者说集合)的标识符
- connected:判断两个节点是否连通
quick-find
用一个一维数组 id[] 存储所有的节点所在连通分量的标识符,每加入一个节点对,就将对应的所有相连节点的标识统一成一个,表示这些节点是连通的。
之所以叫做 quick-find,是因为 find 操作的时间复杂度是 $O(1)$。 而 union 操作需要把当前连通分量的所有节点存储的标识符改为新的,时间复杂度是 $O(n)$。
class UnionFind:
def __init__(self, n):
self.idx = [i for i in range(n)] # 连通分量的标识符,一开始都是自己
self.count = n # 连通分量的数目,一开始都是孤岛
def find(self, p: int) -> int:
return self.idx[p]
def union(self, p: int, q: int):
pRoot = self.find(p)
qRoot = self.find(q)
# 已在相同的连通分量中,无需合并
if pRoot == qRoot:
return
# 不妨将 p 的所有连通的节点改为 q
for i, val in enumerate(self.idx):
if val == pRoot:
self.idx[i] = qRoot
# 连通分量计数
self.count -= 1
def connected(self, p: int, q: int):
return self.find(p) == self.find(q)quick-union
注意到 quick-find 的 union 操作需要遍历数组,每次都要修改很多节点,如何节省这一操作呢?
一种想法是,当加入一个节点对时,直接将两个节点对应的连通分量的标识符连接在一起,即把一个标识改成另一个,而不需要统一所有标识,想象两棵树,只把根节点相连。
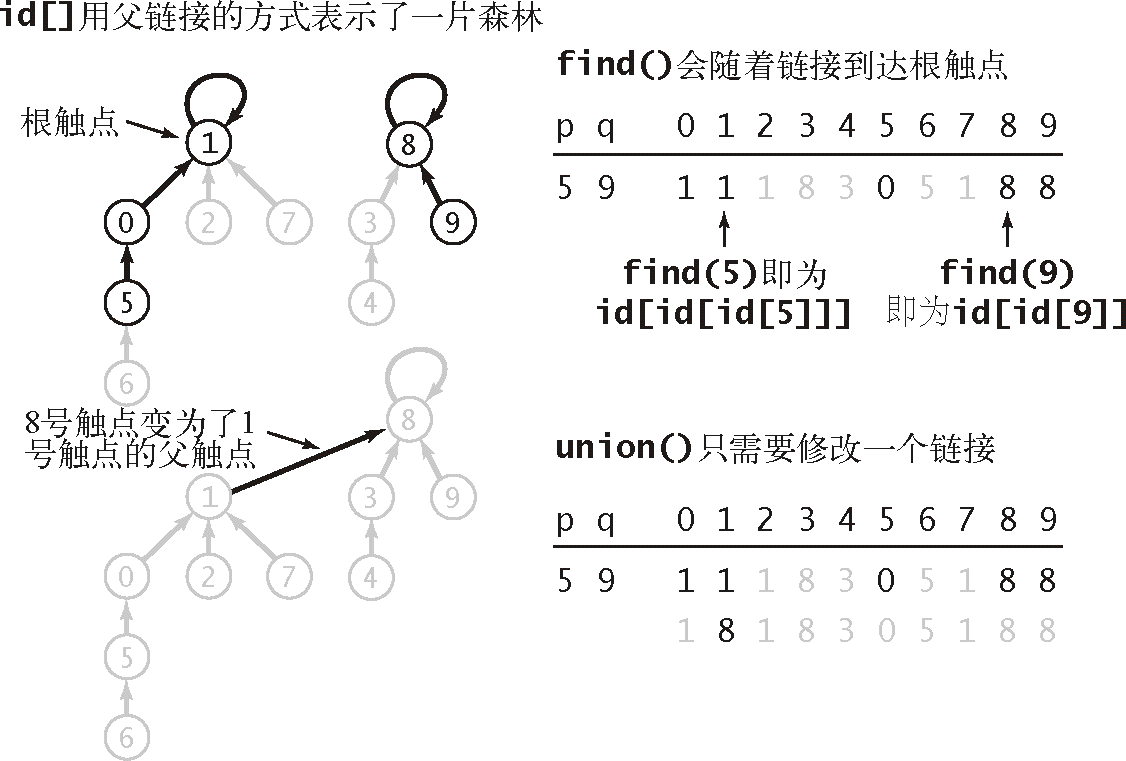
而这却为 find 操作带来了麻烦,一个连通分量有多个标识符,怎么才能找到根操作符呢?为了找到根,需要顺着树不断找父节点,find 的时间复杂度成了 $O(树的高度)$。
quick-union 算法让 id[] 有了新的含义,表示一片森林,加入一个节点对就代表了其中两棵树的相连,每棵树的根节点指向自己。
class UnionFind:
def __init__(self, n):
self.idx = [i for i in range(n)] # 连通分量的标识符,一开始都是自己
self.count = n # 连通分量的数目,一开始都是孤岛
def find(self, p: int) -> int:
# 顺着树,向上找根
while self.idx[p] != p:
p = self.idx[p]
return p
def union(self, p: int, q: int):
pRoot = self.find(p)
qRoot = self.find(q)
# 已在相同的连通分量中,无需合并
if pRoot == qRoot:
return
# 不妨将 p 的根改为 q 的根
self.idx[pRoot] = qRoot
# 连通分量计数
self.count -= 1使用路径压缩的 quick-union
quick-union 算法中的合并思想很好,将节点的相连转化为树根的相连。
理想情况下,判断连通性时,我们希望所有节点都连接上根节点。但又不想像 quick-find 那样每次都修改所有节点。
有一种方法是在 find 的同时将路径上的所有节点都直接连上根节点,这被称为路径压缩,可以用一个循环来改,也可以用递归。使用路径压缩的 quick-union 算法的各种操作的时间复杂度是 $O(log(n))$。
class UnionFind:
def __init__(self, n):
self.idx = [i for i in range(n)] # 连通分量的标识符,一开始都是自己
self.count = n # 连通分量的数目,一开始都是孤岛
def find(self, p: int) -> int:
# 顺着树,向上找根
if self.idx[p] != p:
self.idx[p] = self.find(self.idx[p]) # 路径压缩,递归实现
return self.idx[p]
def union(self, p: int, q: int):
pRoot = self.find(p)
qRoot = self.find(q)
# 已在相同的连通分量中,无需合并
if pRoot == qRoot:
return
# 不妨将 p 的根改为 q 的根
self.idx[pRoot] = qRoot
# 连通分量计数
self.count -= 1有很多介绍并查集算法的文章到这里就止步了,然而时间复杂度还可以再降。
使用路径压缩的加权 quick-union
注意到上一种算法在合并时可能存在比较糟糕的情况,例如总是大树往小树合并,这会导致树是倾斜的。
一棵树的大小 是它的节点的数量。树中的一个节点的深度 是它到根节点的路径上的链接数。树的高度 是它的所有节点中的最大深度。
做一个小的改变就能大大改进算法效率,与其随意地将一棵树连接到另一棵树,不妨将小树连接到大树上,称之为加权 quick-union,再结合路径压缩,最终的算法每次操作的时间复杂度能非常接近常数项。
使用路径压缩(找根的同时把路径上的节点连到根)和按秩合并(将小树合并到大树下)两种优化后,并查集的单次操作(Find 或 Union)的摊还时间复杂度是 $O(α(n))$,$α(n)$ 是反阿克曼函数。这个函数增长得极其极其缓慢,以至于对于所有在实际应用中可能出现的 n(比如宇宙中的原子总数),$α(n)$ 的值都不会超过 5。
为此需要用一个一维数组来记录各个根节点对应的树的大小,每次合并只需要把小树的大小增加到大树上即可。
class UnionFind:
def __init__(self, n):
self.idx = [i for i in range(n)] # 连通分量的标识符,一开始都是自己
self.count = n # 连通分量的数目,一开始都是孤岛
self.size = [ 1 ] * n # 每个连通分量的大小(节点数),一开始都是 1
def find(self, p: int) -> int:
# 顺着树,向上找根
if self.idx[p] != p:
self.idx[p] = self.find(self.idx[p]) # 路径压缩,递归实现
return self.idx[p]
def union(self, p: int, q: int):
pRoot = self.find(p)
qRoot = self.find(q)
# 已在相同的连通分量中,无需合并
if pRoot == qRoot:
return
# 将小树的根改为大树的根
if self.size[pRoot] < self.size[qRoot]:
self.idx[pRoot] = qRoot
# 连通分量的大小修改
self.size[qRoot] += self.size[pRoot]
else:
self.idx[qRoot] = pRoot
# 连通分量的大小修改
self.size[pRoot] += self.size[qRoot]
# 连通分量计数
self.count -= 1相关题目:
- 323. 无向图中连通分量的数目:连通分量计数(基础)
- 547. 省份数量:连通分量计数(基础)
- 200. 岛屿数量:连通分量计数(二维网格),二维网格的一维展开,输入的边需自己构造
- 684. 冗余连接:无向图的成环检测,连接两个已经是同一个连通分量里的节点时立刻成环
- 128. 最长连续序列:利用并查集维护连续区间,数字连续就隐含了一条边,把数字映射到节点编号,找最大的那个连通分量(求连通分量的大小时必须用加权 quick-union)
- 990. 等式方程的可满足性:逻辑推理,处理相等与不等关系
- 1202. 交换字符串中的元素:动态连通性与有序重组
- 721. 账户合并:集合合并与数据整合
总结
从 union-find 算法的不断改进中,可以知道:在设计算法时,往往先简洁而详细地定义问题,然后给出一个简单可行的方案,当问题规模增大时就不得不考虑改进算法了,至于更深入的最优解就交给经验丰富的研究人员吧。