最小生成树：Kruskal算法和Prim算法的实现

这里直接给出离散数学中的几个定理和推论：

• 无向图G具有生成树当且仅当G连通.
• G为n阶m条边的无向连通图，则 m >= n - 1.
• G是树 $\Leftrightarrow$ G中任意两个顶点之间存在唯一路径 $\Leftrightarrow$ G中无回路且m=n-1$\Leftrightarrow$ G是连通的且m=n-1$\Leftrightarrow$ G中没有回路但在任何2个不同的顶点间加一条新边就能在图中得到唯一的含新边的环圈.
• 生成子图指的是顶点集相同，但边集是图G的子集的图.
• 生成树指的是图G的生成子图并且是树.
• 最小生成树指的是图G的所有生成树中权最小的.

算法第4版中这样定义：

• 树是一幅无环连通图。
• 连通图的生成树是它的一幅子图，它含有图中的所有顶点且是一棵树。
• 加权图是一种为每条边关联一个权值或是成本的图模型。
• 一幅加权图的最小生成树（MST）是它的一棵权值（树中所有边的权值之和）最小的生成树。
• 图的一种切分是将图的所有顶点分为两个非空且不重叠的两个集合。横切边是一条连接两个属于不同集合的顶点的边。
• （切分定理）。在一幅加权图中，给定任意的切分，它的横切边中的权重最小者必然属于图的最小生成树。切分定理是解决最小生成树问题的所有算法的基础。

看了一下算法第4版，真的很有帮助，特别是它的几个API的定义，很像ACM模式的输入，对笔试有一定的帮助。

图的表示

邻接矩阵？需要$n^2$的空间，而有百万个顶点的图是很常见的……

邻接表？可以！用一个顶点为键，值为顶点数组，其中的每个元素都是与该顶点相邻的顶点。

此后记住了，咱一般就是用邻接表。

加权无向图的表示

在邻接表的表示中，可以在链表的结点中增加一个权重域。

Prim 算法：横切边

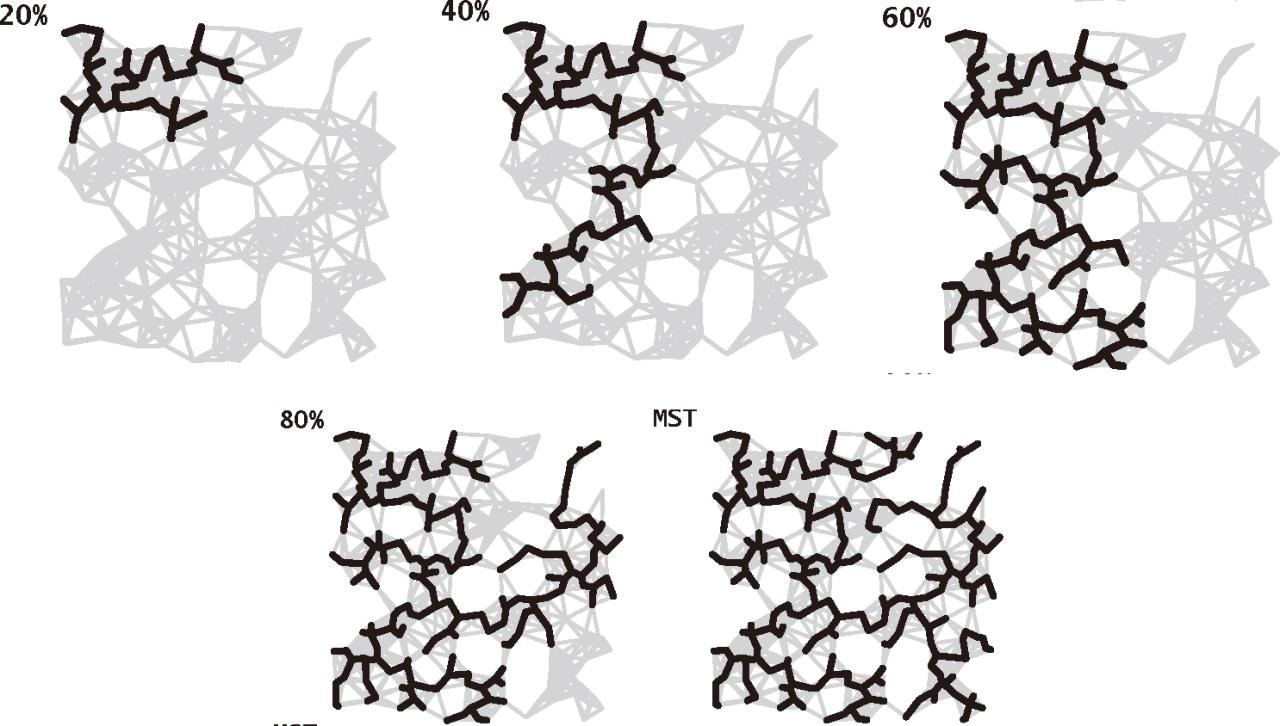
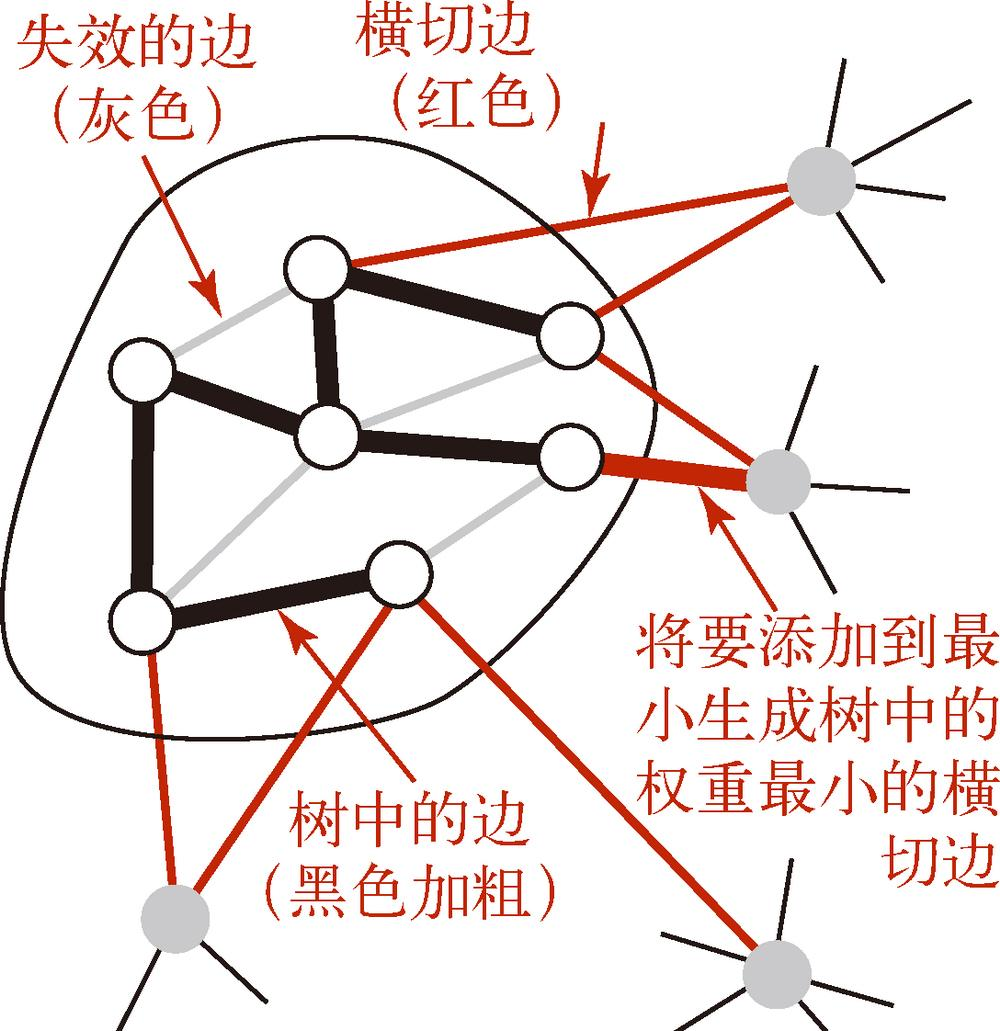
• 初始时只有一个顶点。
• 每一步都为生长中的树添加一条边，总共添加 $V-1$条。
• 每次都是加入一条这样的边（横切边）：连接树中顶点与不在树中顶点并且权重最小的边。

实现思路：

算法第四版给出了两种实现，一种Lazy的，一种即时的。

我们需要一个顶点集合的布尔数组表示某顶点是否在MST中，一个队列来保存MST中的边，还需要用优先队列来根据权重比较横切边。

如何维护横切边的集合呢？每向树中添加一条边也就添加了一个顶点，那么横切边集合将有失效的。此外，我们感兴趣的只是连接树顶点与非树顶点中权重最小的边，因此只需要保存权重最小的那条边，当有顶点进入树的时候，看顶点的引入是否使得权重更小了。

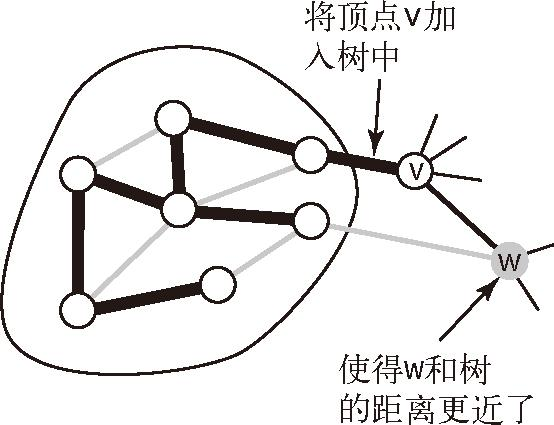
伪代码：

(1) 将顶点0（起点）加入最小生成树，并遍历与起点相连的所有边，将权重最小的放入优先队列pq
(2) while (mstNodeCnt < n) {
		从优先队列pq中取出权重最小的边，将该边加入MST；
		同时将改变对应的顶点V加入MST，并遍历与V相连的所有横切边，找到权重最小的加入优先队列pq;
		mstNodeCnt++;
}

Kruskal 算法：连接一片森林中的两棵树

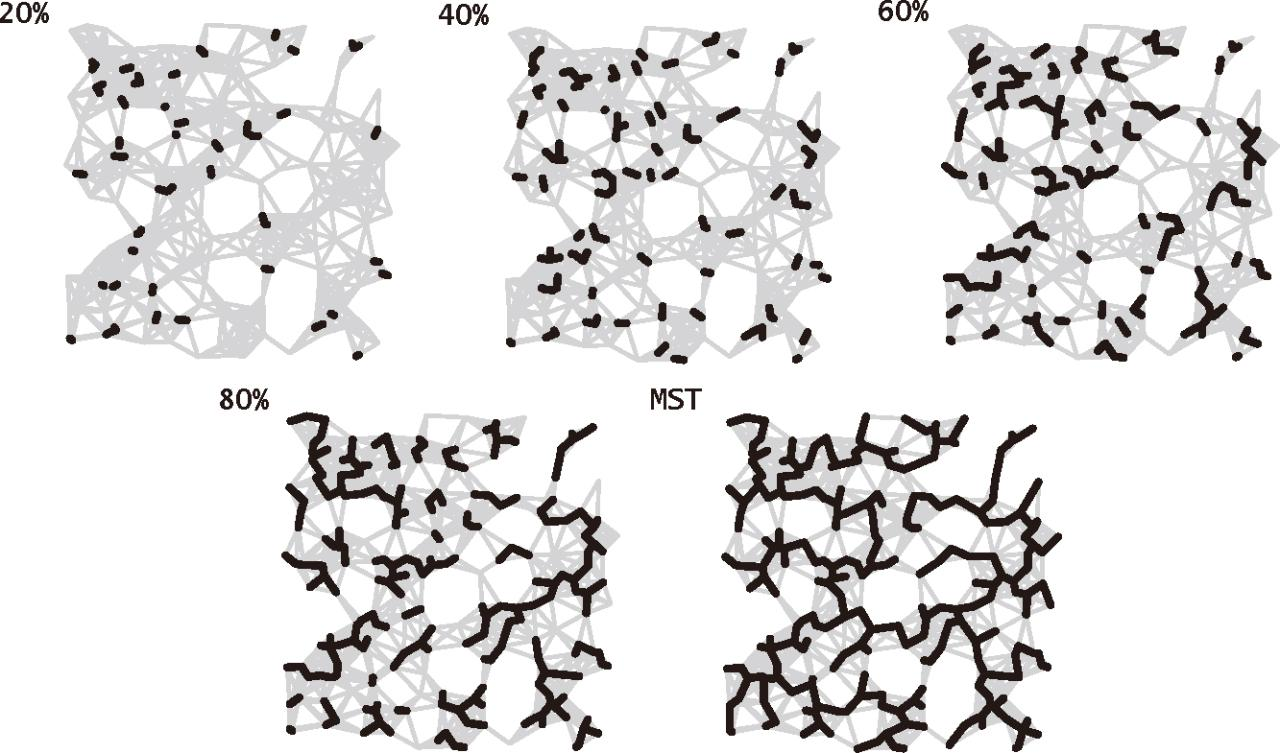
• 初始时选择最小权重的一条边。
• 每一步都为生长中的树添加一条边，总共添加 $V-1$条。
• 每次都是加入一条这样的边：权重最小并且不会和已经加入的边构成环。

实现思路：

我们将会使用一条优先队列来将边按照权重排序，用一个并查集来识别会形成环的边，以及一条队列来保存最小生成树的所有边。

相比Prim算法，我认为 Kruskal 算法实现起来更简单。

伪代码：

（1）对所有的边从小到大排序
（2）while(mstEdgeCnt < n - 1) do{
				取权值最小的边（u，v）；
 				if（u，v不连通）{
						将（u，v）加入T；
						mstEdgeCnt++;
				}
				将边（u，v）从集合E中删除；
    }